Patent: Speculative Decoding with Early Exit for Optimized Transformer On-device Inference

by David Spuler

ABSTRACT

A system and method for executing transformer neural networks allowing optimized on-device inference and reduced computational load for low-power platforms such as smartphones and PCs. Specifically, a novel method of combining parallel decoding algorithms, such as speculative decoding, with early exiting of layers is defined. This optimization improves efficiency of these decoding algorithms in parallel execution, and also notably makes them more efficient in sequential execution. Improved sequential efficiency arises from directly analyzing a reference token sequence using transformer-calculated probabilities to assess acceptance of a token. The optimization relies on a novel, improved early exit algorithm that is faster and more accurate by using reference tokens in the exit decision logic of the verification model, such as by analyzing draft tokens in speculative decoding.

TECHNICAL FIELD

The present invention relates generally to transformer neural network architectures in artificial intelligence, and more particularly to optimizing the speed of transformer inference, in both parallel and sequential execution, on both high-end data center GPU computers and low-resource computing devices such as smartphones, tablets and laptop computers.

BACKGROUND OF THE INVENTION

Artificial Intelligence (AI) is the field of designing software and hardware systems to make computer-based systems appear to act intelligently. Natural Language Processing (NLP) is the subset of AI involving understanding or creating natural language in text form.

The current state-of-the-art architectures for many NLP tasks use a transformer architecture as the computation engine and a model such as a Large Language Model (LLM) with billions of weights. A well-known example is the ChatGPT product using a Generative Pre-trained Transformer (GPT) architecture.

Transformer architectures are general-purpose neural network architectures that can be used for a variety of NLP tasks. For example, a transformer architecture may receive input text representing a question and generate output text representing an answer. As another example, a transformer architecture may receive input text representing a document and generate output representing an edited version of the input document. As yet another example, a transformer architecture may receive input text representing a document and output text representing a summary of the input document.

Transformer architectures may perform inference in different computer system architectures with one or more computer devices, and with or without a network. As one example of a computer system architecture with multiple computer devices and a network, the transformer architecture may execute inference in cloud backend system in an online system. In this case, users submit input queries remotely over the network to the transformer architecture that executes inference in one or more computer devices, which are called "servers" in the "data center". After computation by the transformer architecture, users then receive their output results back again via the network.

As another example of a computer system architecture with one computer device, the transformer architecture may execute inference on the same computer device that is used for user input, such as a user's smartphone, tablet, laptop computer, or desktop computer. The use of a transformer architecture in this way is called "on-device inference" because the transformer executes the inference computations directly on the user's device without needing network transmission. The transformer architecture's computations are returned to the user as output on the same device.

The primary problem with transformer inference is the heavy computation costs for expensive computing power, such as with CPUs and/or GPUs, which is both costly and often results in slow response time latency and low throughput. Running transformer inference in a data center uses extensive GPU resources. These computation costs also make it difficult to efficiently run transformer-based inference on low-resource devices such as smartphones, tablets, and laptop computers, with adequate speed and response time. This efficiency problem is true of many transformer-based use cases in general.

Beyond costly and slow computations, accuracy of output results is a concern. Transformer architectures have various accuracy limitations, such as hallucinations (false information), difficulty with mathematical reasoning, and the use of integrated add-on tools to correctly answer various types of queries.

One of the modules in a transformer architecture that can affect both efficiency and accuracy is the decoding algorithm. This is the tail-end optimization that chooses a token to output, after the predicted probabilities have been calculated. Making a correct choice in this decoding algorithm is useful for accuracy, and also for efficiency, because of the autoregressive algorithm used in transformer decoder stacks, whereby the decoder stack is executed sequentially in recurring iterations as controlled by the decoding algorithm at the end of each decoding cycle. Hence, the decoding algorithm has a disproportionate influence on the total speed of the transformer architecture.

Several ways to optimize the decoding algorithm via parallel execution have been proposed in the prior art. Speculative decoding uses a smaller "drafting model" to predict multiple future tokens, which are "verified" by the larger model in parallel. Lookup decoding has a similar type of parallelism, but replaces the drafting model with a search through a datastore of document excerpts, or searching the context tokens of the input prompt directly. Blockwise parallel decoding is also similar to speculative decoding, but its drafting model produces multiple tokens in parallel, whereas speculative decoding calls the smaller model repeatedly in sequential execution. Aggressive decoding also uses the same parallel verification, but its drafting sequence is the input tokens from the prompt.

One of the disadvantages of these parallel decoding methods, such as speculative decoding, is that although they can be faster in wall clock terms, they achieve this speedup by performing extra computation. Hence, a GPU-based implementation of parallel decoding will cost more by increasing the total load on the GPUs, although it is spread across multiple GPUs by parallelization.

Another major disadvantage of parallel decoding is that it requires parallel computation to be effective. These methods are a de-optimization when used with sequential execution. Hence, platforms such as on-device inference on laptops and smartphones cannot benefit from these parallel decoding algorithms. Even to the extent that a smartphone may have some parallel computation capacity, such as a Neural Processing Unit (NPU) or low-end GPU, the aforementioned increase in overall computation loads may overload a low-resource phone, and cause "frozen phone" problems, overheating, and/or battery depletion.

Optimizing the decoding algorithm is one area in which to speed up transformer architectures. Many other approaches to optimizing transformer architectures are described in the literature, such as quantization, pruning, and GPU vectorization, most of which are orthogonal to the use of faster decoding algorithms, meaning that the two optimization methods can be combined. Adaptive inference optimizations are a subset of transformer optimizations, whereby the computation pathway for inference is changed at runtime, depending on the input text.

Early exiting of layers is one such method of adaptive inference optimization, which is generally applicable to many transformer-based use cases. The idea is to exit computation of the decoder layer stack early, thereby avoiding many millions of computations from the skipped layers. Early exit optimizations are approximations that reduce the accuracy of results. Furthermore, the complexity within the exit decision logic can make them less than optimally efficient by not detecting all cases where they could exit and skip layers of computation.

SUMMARY OF THE INVENTION

The present disclosure examines methods to speed up transformer architectures in computing results of inference, particularly by optimizing the decoding algorithm at the end of each layer. Certain features of the disclosure also increase accuracy of results, by focusing the decoding algorithms more fully on a sequence of reference tokens.

Although effective for transformer architectures running on any systems, this disclosure is particularly relevant to executing tasks on low-resource devices such as smartphones and personal computers, because it can speed up sequential on-device inference for CPU execution without a GPU, as well as improving efficiency of parallel execution in larger data center computers with powerful GPUs.

There are several parallel decoding methods that utilize a reference token sequence in their optimizations. For example, speculative decoding uses a draft model to generate draft tokens, which can be used as the reference sequence herein. The availability of these reference tokens offers the opportunity for novel further optimizations to their algorithms.

Parallel decoding algorithms, as their name implies, were originally aimed to increase efficiency of parallel execution of transformer inference, such as on GPUs in data center servers. The present disclosure offers ways to further increase their efficiency in parallel execution.

However, parallel decoding algorithms in the prior art were not useful for sequential execution, such as for on-device inference on laptop computers and smartphones, because they increased overall load. The disclosure herein increases efficiency of these decoding algorithms not only in parallel execution, but also offer a new way to run these decoding algorithms efficiently in sequentially-executed code in low-resource environments.

The present disclosure demonstrates these novel methods: (a) the method of combining the parallel decoding algorithms, such as speculative decoding, with an early exiting method of layer optimizations, to further speed up transformer inference, (b) a novel use of a reference token sequence, such as via reference token probabilities or ranking, in the decision criteria of an early exiting method, which makes an early exit optimization method faster and more accurate than prior art, with broad applicability to many transformer use cases, and (c) the further modified parallel decoding methods using a combination whereby this novel early exit decision logic, which is based on reference tokens, is integrated with the parallel decoding methods.

In order to further optimize a parallel decoding algorithm, it can be combined with early exit of layers in the transformer. This combination is faster than the parallel decoding algorithm alone, because it is a dual speedup using two distinct techniques. Many of the variants of early exit, with their various types of decision logic, can be orthogonally used with parallel decoding. For example, a simple exit decision criteria would be to exit whenever the model is predicting its next token with a probability over a threshold of 90% probability.

This early exit algorithm can be even further optimized through a novel integration between the parallel decoding algorithm and the decision logic for early exiting. The extra information available in a reference token sequence, such as the draft tokens in speculative decoding, allows the early exit decision algorithm to directly use the reference tokens and their probabilities in its logic.

In a number of decoding algorithms, there is extra information available in a reference token sequence to optimize the early exit decision module. Hence, the transformer architecture can exit earlier in its layers, and more often, with further efficiency gains when there is a direct match between the reference tokens and the layer logits.

Early exit is an approximation, improving speed at a cost to output results. Hence, the use of early exit with a decoding algorithm comes with some decline in terms of accuracy of the model output due to layers being skipped at runtime.

This novel early exit decision method using reference tokens also improves accuracy. The early exit logic can also be extended to become more accurate in terms of when to exit layers with output tokens by examining the reference token sequence.

Certain features of the present disclosure can be combined and used together for further optimizations. Another aspect involves combining parallel decoding algorithms with the early exiting methods, and furthermore, with the specialized version of early exiting using a reference token sequence.

BRIEF DESCRIPTION OF THE DRAWINGS

FIG. 1 is a high-level block diagram of a system environment for an online cloud system, in accordance with a number of embodiments of the present disclosure.

FIG. 2 is a high-level block diagram of a computer device, such as a computer server, smartphone or laptop computer, in accordance with a number of embodiments of the present disclosure.

FIG. 3 is a block diagram of a system for transformer inference, in accordance with a number of embodiments of the present disclosure.

FIG. 4 is a block diagram of an input module for a transformer, in accordance with a number of embodiments of the present disclosure.

FIG. 5 is a block diagram of an output module for a transformer, in accordance with a number of embodiments of the present disclosure.

FIG. 6 is a block diagram of an encoder-decoder transformer architecture, in accordance with a number of embodiments of the present disclosure.

FIG. 7 is a block diagram of a system for QKV attention in a transformer, in accordance with a number of embodiments of the present disclosure.

FIG. 8 is a block diagram of a Feed-Forward Network (FFN) module, also known as a Multi-Layer Perceptron (MLP), in accordance with a number of embodiments of the present disclosure.

FIG. 9 is a block diagram of a Multi-Head Attention (MHA) module, in accordance with a number of embodiments of the present disclosure.

FIG. 10 is a flow-chart of a method for autoregressive decoding in a transformer, in accordance with a number of embodiments of the present disclosure.

FIG. 11 is a flow-chart of a method for early exit optimization of a transformer, in accordance with a number of embodiments of the present disclosure.

FIG. 12 is a flow-chart of a method for speculative decoding of a transformer, in accordance with a number of embodiments of the present disclosure.

FIG. 13 is a flow-chart of a novel improvement to the early exit method, extended by reference token decision optimization, in accordance with a number of embodiments of the present disclosure.

The figures depict various embodiments of the present invention for purposes of illustration only. A person skilled in the relevant art will readily recognize from the following discussion that alternative embodiments of the structures and methods illustrated herein may be employed without departing from the principles of the invention described herein.

DETAILED DESCRIPTION OF EMBODIMENTS

The present disclosure relates generally to a transformer architecture, whereby many embodiments involve the use of a transformer engine method, consisting mainly of executable instructions, and an associated LLM model, consisting mainly of data. Features of the disclosure herein may be applied to improve the efficiency and accuracy of inference with such a transformer architecture.

Embodiments of the present disclosure may be implemented on a number of computer systems with different system environments or hardware architectures. In one embodiment that is used in commercial systems such as ChatGPT, the computer system involves a cloud-based architecture and a network, whereby the users communicate with a cloud-based AI system from their own user devices over the network. In another embodiment, the method may be performed on a computer system that is a single computer device, such as a personal computer, laptop, or smartphone. In yet another embodiment, the computer system may involve a hybrid architecture where some processing is performed on a user device and some processing is performed in a cloud-based system.

Transformer Architecture

Numerous different embodiments are possible using different transformer engines and different LLMs. Although some specific embodiments of transformer architectures are described in detail herein, there are many variants, extensions, and modifications that are used in the prior art, and continue to be created, and many of these embodiments are orthogonal to the features disclosed herein, allowing them to be used as embodiments of the invention. Similarly, there are many types of LLMs, both large and small, and having different structures, which can be used in embodiments of this invention.

The details of transformer architectures, including numerous variations, are well-known in the research literature, in commercial products such as OpenAI's ChatGPT and Google's Gemini, and also in fully-coded open-source transformer architectures and LLMs with billions of weights available for free on the internet. A brief discussion will be given here of transformer inference algorithms to motivate the improvements that the present disclosure describes, including improved efficiency by utilizing specialized features of a reference token sequence.

In many embodiments, the transformer engines are executable algorithms, and the models are files containing static data, including numeric weights that have been pre-calculated in a training phase using training data sets.

The methods for creating LLMs using training or fine-tuning have an extensive literature base. Many different training methods may be used to create an LLM to use with a transformer engine in an embodiment of the present invention.

Inference is the process whereby a transformer engine uses a model, which has already been trained, to answer an input query by creating an output response. The weights in the model are not usually changed during inference calculations.

The first major transformer in 2017 had two main components, an encoder and a decoder, and was called an encoder-decoder architecture. Subsequently, variants have been discovered including encoder-only architectures (without a decoder) and decoder-only architectures (without an encoder). Most state-of-the-art transformer architectures now use decoder-only architectures, such as GPT, although encoder-only and encoder-decoder architectures still have some relevant use cases.

Both the encoder and decoder major components consist of multiple layers, called the "encoder stack" and "decoder stack," respectively. An encoder-only architecture has no decoder stack, and a decoder-only architecture has no encoder stack. The number of layers in any stack may vary according to the model size and this is usually decided prior to training.

In many embodiments, each layer within each stack is identical in structure, with the same number of weights (but different values) and the same sub-components in each layer. However, other embodiments involve transformer variations where layers in the same stack can have different dimensions or structures.

Computation within each layer stack progresses one layer at a time. The output from one layer is used as the input to the next layer. After the final layer, the layer stacks are finished, and final output processing is performed.

Tensors are used for faster computations in transformer architectures, for both the attention and FFN computations. Tensors are multi-dimensional arrays of numeric data, where a vector is a one-dimensional tensor, and a matrix is a two-dimensional tensor.

Each layer in the decoder stack consists of sub-layer components with two main types: (a) attention heads and (b) Feed Forward Networks (FFNs), also sometimes called a Multi-Layer Perceptron (MLP). Other sub-layer components include normalization modules, addition modules, activation functions, and Softmax. The encoder-decoder architecture also has a cross attention module to coordinate between the encoder and decoder.

Each attention head in the transformer architecture consists of three major weight matrices, denoted as Q (query), K (key), and V (value). Attention heads may implement a self-attention algorithm or a masked attention algorithm, depending on in which stack they are located.

One well-known optimization to the QKV attention algorithm that is used in many embodiments of transformer architectures is called "KV caching." This involves a method of storing caches of the K and V tensors from one token cycle in the memory or secondary storage, and then subsequently to re-use this data in the next token decoding cycle by loading the data from memory or storage.

The FFN components also contain sub-components. In modern transformer architectures, FFN modules consist of two linear layers, each involving matrix multiplication using weights in a matrix, followed by an addition of a "bias" vector using different weights, with an intervening activation function module between the two linear layers. Many well-known activation functions may be used in a transformer architecture, such as RELU, GELU, ELU, Swish, tanh, and others in the prior art, of which RELU is more efficient to compute.

Before any of the layers are executed, there are initial input processing steps. The steps include tokenization of the input text into a sequence of tokens (integral numbers) based on pre-defined token strings called the "vocabulary" of the model (e.g., 50,000 different strings).

The next step after tokenization is converting each of these single-number tokens into a vector representation called "embeddings" (usually via multiplication by an embedding matrix, learned during training), thereby creating a vector of vectors, which is a matrix. One dimension is the embedding vector size and the other is the token sequence length, or length of the maximum context window if this is less than the sequence length. This embedding representation is then merged with positional embeddings (based on cosines or other variations), and then this matrix is passed into the first transformer layer.

Transformer inference runs in two major phases. In encoder-decoder architectures, the first phase is the encoder, and the second phase is the decoder. In decoder-only architectures, the first phase uses the decoder stack to perform an encoder-like function and this is called the "prefill" phase. Both of these phases are computation-heavy as they process the entire input sequence, and one cause of inefficiency and slow response times is the encoding or prefill phases of inference. This first major phase of encoding or prefill is usually preparatory, such as to create the internal representations and KV caches for the input text, and does not output a token for an encoder, or may output the first token for the decoder-only prefill phase.

The second major phase in both encoder-decoder and decoder-only architectures is called the "decoding phase", and in its best-known embodiment involves selecting an output token one at a time, which is called an "autoregressive decoding algorithm." For encoder-only architectures, the second major phase is not similar to the autoregressive decoding algorithm, and there are various other well-known post-encoding computations possible.

After the layers have been computed, there is a final output processing stage that emits a single token. The calculated results from the layers are still in embeddings format, requiring an "unembedding" step that converts the embeddings back to token probabilities via a linear layer (i.e. matrix multiplication and optional bias).

This vector of values from the unembedding computation is then processed by Softmax normalization to create a valid probability distribution of the predicted token probabilities (called "logits"). The output of Softmax is a vector of probabilities, with one value for each token in the vocabulary, where each probability is in the range [0,1] and the token probabilities sum to one.

A decoding algorithm is then used to analyze the probability distribution of the tokens, and to choose one of these tokens to emit. The present disclosure includes demonstration of some enhancements to decoding algorithms and they are examined in further detail below.

Decoding Algorithms

The present disclosure relates to improvements to decoding algorithms, when executing in parallel or sequentially. The availability of a reference token sequence in many decoding algorithms allows a novel decoding algorithm to be more efficient than general-purpose decoding algorithms.

The decoding algorithm is the last step in a transformer before outputting a token. Decoding algorithms in transformer architectures work as follows. One full cycle of transformer inference, as described above, outputs a vector of probabilities that indicate which token should be output with what predicted probability. The decoding algorithm is the method whereby the transformer chooses a token to output from that list of probabilities.

There are several types of decoding algorithms known in the prior art, most of which are generally applicable to many use cases. The greedy decoding algorithm simply chooses the token with the maximum probability. The top-k decoding algorithm chooses randomly between the k tokens having the highest probabilities, which is more flexible and creative than greedy decoding. The top-p decoding algorithm modifies top-k decoding to avoid choosing any tokens with probabilities below a threshold, which may involve choosing from less than k tokens. These decoding algorithms usually consider the probabilities of one token position without any "lookahead" to future words.

Beam search decoding is another well-known decoding method that is more advanced as it uses "lookahead" to defer the decision on which tokens to output until it has seen more than one token ahead, which can be more accurate in outputing multi-word phrases of multiple tokens.

The main problem with these decoding algorithms is that they are inefficient because they are "autoregressive" algorithms, whereby any token that is output, is then reprocessed as input by the entire transformer in the next decoding cycle. For example, when the transformer has already processed N tokens, the autoregressive algorithm performs the steps: (a) generate the N+1th token from intermediate output tokens 1..N, with a full cycle of the transformer stacks, involving billions of computations; (b) for the next token, the N+2th token, the N+1th token is added to the intermediate output, and the tokens 1..N+1 are used in a full transformer cycle to produce the N+2th output token.

Only one token at a time is produced, sequentially, by this autoregressive decoding method. The topmost progression of this algorithm cannot be sped up by parallel computation because each decoding cycle is waiting on the output token from the prior decoding cycle. GPU chips can parallelize many lower-level computation steps within each transformer cycle, but this major high-level bottleneck in the decoding algorithm is hard to overcome.

There are various methods in the prior art that create "non-autoregressive" or "parallel decoding" algorithms, such as speculative decoding, lookup decoding, or aggressive decoding. Aggressive decoding is specific to grammatical error correction (i.e., "editing" of a text), whereas the others relate to general transformer use cases.

Speculative decoding repeatedly does a two-step method for each full inference cycle. It is a "draft and verify" approach. The first step is to draft a sequence of tokens using an efficient, small model. The second step is to "verify" these with the main model, which is called the "verifier" model, and is a larger model, such as the main model that is to be optimized.

The draft model that creates a reference token sequence is usually a smaller model, which can be a model with smaller dimensions, a compressed model, or a model with various optimizations. This draft model is simply run with normal transformer inference cycles, repeatedly in sequence, to generate a number of draft tokens, which are effectively predictions.

Note that the multiple calls to the draft model cannot be parallelized if it is a normal, autoregressive model. However, these predictions are less costly to compute, since it's a smaller model. They are also likely to be less accurate than the larger verifier model (i.e., the main model), but should still be reasonably accurate, since the draft model is still a capable model.

The number of tokens in a draft sequence vary, and require some testing dependent on the small model's abilities. The general rule of thumb is that 75% of tokens are "easy" and can thus be predicted by a smaller model, whereas 25% will be more difficult. Hence, the draft length is usually a small number (e.g., 5 or 10 tokens), because the draft model is less likely to be fully accurate on long sequences. For example, the draft model might be programmed to generate a sequence of 10 tokens as the suggestion for the draft token sequence.

The next step of speculative decoding is to perform a full inference cycle on the main model, called the "verifier" model, for all of the 10 draft tokens. After all 10 tokens have been computed in parallel by the verifier, the results of these 10 inference cycles of the large model are compared against the draft tokens from the smaller model. The prefix sequence of tokens that match is output by the model, and the remainder are discarded. For example, if six tokens matched, but the seventh does not, then six tokens are output, and four are discarded, with an overall speedup of six times due to parallelization.

This sequence repeats again until the full output has been repeated. At every step, up to 10 tokens could be emitted in parallel, giving a large speedup in wall clock terms. However, there is wasted computation for any of the draft tokens that did not match and are thus discarded. Also, there is a net loss if the draft model fails to predict the first token, or only predicts one token successfully. On average, the draft model should be more accurate than not, and the more tokens it can get verified, the faster the overall process.

A practical point for speculative decoding is that the smaller draft model and the larger verifier model must use the same tokenizer. Both the text strings and numbers used for tokens must match in order for the draft tokens and the verifier's output tokens to be compared. Similarly, the tokenizer of the retrieval methods in lookup decoding must match the verifier model.

One of the disadvantages of speculative decoding is that the total amount of computation is actually higher, even though the wall clock time of inference may be reduced. There is extra computation done in parallel, so that the amount of GPU resources used by speculative decoding is higher than without using its parallelism. There are two sources of extra computation: (a) the cost of the draft model, although this is usually less expensive than the bigger verifier model, and (b) the extra cycles of full inference done on the larger verifier model, including some wasteful cycles for draft tokens that fail and are discarded.

Another major disadvantage of speculative decoding is that it cannot optimize sequential execution of inference. Since there are extra cycles of transformer inference performed by speculative decoding when performed in parallel, if these are done sequentially, then it is a de-optimization that will increase the time required to perform inference. For this reason, speculative decoding is not very useful for on-device inference on low-resource platforms lacking in parallel capabilities, such as laptop computers and smartphones. Note that the improved version of speculative decoding disclosed herein can reduce the number of layers computed in parallel execution, thereby reducing the extra load on GPUs in large-scale data center inference.

Note that there is no value in speculative decoding if the draft model only predicts a single token. The value of parallelization occurs when two or preferably more tokens can be verified in parallel.

The value of the improvement disclosed herein is in the larger verifier model, whereby early exit can reduce the cost of the full decoding cycle in the larger model. This approach means that modified speculative decoding may still be an optimization for even a single draft token, and also that there may be value in sequential execution, because the novel early exit logic can reduce the number of layers, even if computed sequentially.

In other embodiments of speculative decoding, the draft model can be other types of neural network architectures, such as an optimization of the larger model (e.g., by quantization, pruning, early exit, etc.), or another approximation or compression method applied to a large model.

Blockwise parallel decoding is similar to speculative decoding, but the drafting model is modified to predict multiple draft tokens in parallel (i.e., rather than by multiple sequential calls to the small model). Hence, the drafting model has a different architecture, whereby it has been trained to predict multiple tokens, but the verifier model is the same approach. As for speculative decoding, the verification is performed by a large model (in parallel), and the prefix subset of tokens that match are emitted as output.

Lookup decoding involves searching for a reference token sequence in a set of documents or a datastore by searching for a subsequence. The idea is that the model may emit sub-sequences of tokens that are directly quoted from documents on which it was trained or fine-tuned. Hence, lookup decoding gets its reference token sequence from existing documents, rather than newly generating a sequence. Note that the external document text will need tokenization, or perhaps may be stored in a pre-tokenized format as a further optimization.

A subtype of lookup decoding is "prompt lookup decoding," which involves finding a reference token sequence in the context of the prompt input, by searching for a subsequence. This approach is particularly applicable to RAG architectures, whereby chunks of text from external documents are usually prepended to the input prompt as context. Hence, the idea is to search the prompt text for a sub-sequence that the model might emit verbatim as part of its answer. Searching in the sequence of tokens in the prompt text is more efficient than using a model to create draft tokens, even if it is a small model. Note that the prompt text has already been tokenized in creating the input tokens, so the only cost is the search to find a token sub-sequence, which involves scanning a linear list of integers (i.e., the token values).

One aspect of both lookup decoding and prompt lookup decoding concerns how many tokens to search for. The simplest approach is to scan for a single token, specifically the most recently emitted output token, in the current output sequence. This is efficient, but will have many false matches. More accurate, but slightly less efficient, is to search for the prior two output tokens, or three tokens or more, which will give more accurate matches. However, using a search for too many emitted output tokens will only rarely match, and not lead to much efficiency gain. The optimal value will depend on the documents in the datastore for lookup decoding, and the RAG text chunks in the datastore for prompt lookup decoding, and will require testing to determine.

Both types of lookup decoding are effectively subtypes of speculative decoding, whereby the draft model is replaced with lookup searches. These reference token sequences are then verified in parallel, with those that match emitted as output, as for speculative decoding.

Aggressive decoding refers to using the full sequence of input tokens as a reference token sequence, which is then validated by a larger model using parallel computation. It can be thought of as a type of speculative decoding whereby the "draft" tokens are simply a subsequence of the input document, and verification by a large model is performed in parallel, followed by the same method of outputing the prefix of tokens that match, as for speculative decoding. This reference token sequence is readily available in the input token sequence, without the extra cost of a "draft model" as in speculative decoding.

To find the reference token sequence in the input tokens, the aggressive decoding algorithm can simply keep track incrementally of the current location within the input tokens, in comparison with the output tokens. However, in some cases this synchronization is difficult to maintain, or may be complicated by additional instructions prepended or appended to the context. Instead, the method can perform a search of the input token sequence in a manner similar to prompt lookup decoding to find the starting point for the reference token sequence.

One problem with these prior art parallel decoding algorithms is that several use an additional second transformer model, called a "draft model," which is usually smaller and faster than the main transformer, but executing the draft model is nevertheless extra processing overhead.

These parallel decoding methods perform extra processing in parallel across multiple GPUs, aiming to speed up the latency (response time) for the user. Although this is faster in wall clock terms, it actually increases the overall GPU processing load (in parallel), making it more costly to run.

Furthermore, these prior art parallel decoding algorithms are not effective in low-resource on-device inference, such as smartphones, where there are not multiple GPUs to perform parallel processing. Even to the extent that a device has some parallel execution capability, such as in the CPU's SIMD instructions or a Neural Processing Unit (NPU), it is unlikely to have enough capacity. Even if it does, then the overall increase in load from parallel processing will overload the device, causing problems such as a "frozen phone," overheating, or battery depletion.

The present disclosure of improvements to parallel decoding methods relates to improving the last module used in each inference cycle (i.e. the decoding algorithm module), which is orthogonal to the rest of the transformer software architecture. Decoding algorithms including the present disclosure may be used for encoder-decoder, encoder-only, and decoder-only transformer architectures. Furthermore, decoding algorithms may be used on any past or future transformer variants or non-transformer software architecture, whether neural network or otherwise, provided that it computes probability predictions about the next token to emit.

Early Exit

Early exiting of layers involves exiting processing in a layer stack before the remaining layers have been computed, so as to speed up transformer execution. Research has found that the initial layers tend to make the big decisions about tokens, whereas the final layers are usually finessing between a few acceptable tokens. This motivates the idea to stop computing layers as soon as a layer has computed a viable output token. This is a dynamic adaptive inference optimization, with the decision to exit made at runtime, rather than statically by permanently removing some layers from the model file.

Adding early exit of layers to a transformer architecture is relatively easy. It is convenient because each layer of a model has the same size input and output, so any layer's output can be sent to the unembedding module and, if exiting, then to the final output processing steps. However, one of the downsides is the additional computation for "unembedding" and exit decision logic at potential layer exit points, but this is usually less than the gain from skipping layers.

In a transformer without early exit, the unembedding logic takes place after the layers have been computed. Unembedding involves a linear transformation using an "unembedding matrix" and a Softmax normalization to convert the embedding vectors into numeric token probabilities for each token, which are called "logits" and are output as a vector of probabilities for each token in the vocabulary. The unembedding matrix can be the matrix inverse or matrix transpose of the embedding matrix.

Softmax normalization is a well-known method that normalizes the unembedding values into a valid probability distribution, where each value is in the range [0,1] inclusive, and the probabilities sum to one. The Softmax method involves (a) exponentiating each vector element, (b) computing the sum of these exponentiated values, and (c) scaling each element of the new vector by this sum.

In an early exit transformer, the unembedding logic may be added to any layer where the model may decide to exit early, along with an "early exit decision" logic module that decides whether to exit at that layer. For early exiting after a fixed number of layers, the decision logic is simply a comparison of the layer count against a fixed number, without using the token probabilities, and therefore does not use an extra unembedding calculation. However, early exit decision modules that are based on token probabilities use the probabilities calculated as "logits" by an unembedding module and Softmax module at that layer.

Another implementation detail is that early exiting causes problems with the KV cache optimization. Any layers that are skipped by exiting early do not get their KV cache computed in that decoding cycle, and will be out-of-date in the next token's decoding cycle. Whenever an early exit is taken, any layers that are skipped have the cache marked as out-of-date.

Several methods to do early exiting without disrupting the KV cache are reported in the literature including: (a) recomputation, (b) propagation, or (c) prevention. One method is simply recomputing out-of-date KV caches when detected, although this is inefficient from the recomputations and tracking out-of-date KV cache values.

More efficient than recomputation is propagating the current layer's KV cache data to the skipped layers when early exiting, which ensures there is a KV cache, but the cached values from a different layer are an approximation of the cache that would have occurred if the remaining layers were fully executed. This propagation method is efficient by avoiding recomputation, and the byte copying for propagation can optionally be further optimized by using a pointer or offset method of indirection to track which layers of the KV cache should get which data blocks from the KV cache.

Even more efficient than correcting the KV cache after early exit is modifying the early exit algorithm to completely prevent out-of-date KV caches from occurring. For example, this is possible by: (a) using early exit after a fixed number of layers or (b) exiting after a monotonically decreasing layer count as the token sequence progresses. Another possibility on systems where the KV cache memory is excessive is simply to avoid using a KV cache at all.

Early exiting aims to be faster because it simply does not compute some of the layers, which may involve many millions of weight computations. However, it damages the accuracy of the results of the transformer, meaning that the output text is not as good as the full non-exited layer stack. Hence, various decision methods have been developed to decide whether or not the currently predicted tokens are accurate enough to allow an early exit.

Various methods of implementing early exit have been reported in the research literature, with the decision to exit a layer based on logic such as: (a) exiting after a fixed number of layers, (b) exiting when there is a token with a high-enough predicted probability, (c) exiting when the predicted probabilities of the tokens are stable between layers, (d) exiting when the difference between the highest and second-highest predicted probability is above a threshold, and (e) numerous other minor variations on these methods.

Reference Token-Based Early Exit

The present disclosure demonstrates an advanced version of early exit whereby the decision logic incorporates the probabilities or rankings of tokens in a reference token sequence. This novel approach of focusing early exiting decisions on reference tokens improves overall efficiency by often allowing earlier exiting than with prior art early exit decision algorithms. The percentage of early exit modules that decide to exit early is increased, which increases the number of skipped layers, thereby improving the overall efficiency of the transformer architecture.

The predicted probabilities of the reference tokens are available for early exit modules. The logits for tokens are known after any layer, whereby the "unembedding" and Softmax calculations are performed after the layer is calculated. Hence, the probability for the current reference token within the decoding algorithm is immediately available in the logits. The decision logic can use a test based on a probability threshold or a top-N ranking for the current reference token. The threshold value should usually be low (e.g., 5%) or the N value for the top-N ranking be high (e.g., top-20), because there are often many valid tokens at a given point in inference.

A full unembedding computation via an unembedding matrix is used to compute the logits, even though this early exit criteria can use the probability of a single token, the current reference token. It is possible to get a single numeric value by a vector dot product of the current embedding vector multiplied by the unembedding matrix row specific to the token number of the current reference token. However, this value is not a probability, but is a log-scale number of unclear significance because its relative magnitude to other results is unknown. This value is exponentiated and then scaled using the sum of the exponentiated values in the Softmax module. Unfortunately, the full unembedding matrix computation is used as input to Softmax normalization, so as to compute the predicted probability of the single reference token. Hence, the method of using a single reference token's probability does not make the unembedding calculation for early exit any faster, but can nevertheless improve decision accuracy, which allows exiting at an earlier layer, thereby improving overall model efficiency.

The use of reference tokens in early exit decision logic is specific to decoding algorithms where there is a reference token sequence. General decoding algorithms without a reference token sequence have no tokens to compare against when examining the logit probabilities. Hence, the decoding algorithms with a reference token sequence can use reference token-based early exit and add more specific logic to the early exit criteria such as: (a) whether the reference token has a predicted probability higher than a threshold, and/or (b) whether the reference token is amongst the top-N predicted logits.

As an example, a generic early exit criteria might be to exit when the predicted token is 80% probability. However, the advanced early exit decision test using reference tokens could set a lower threshold to allow the early exit if the reference token has a 20% probability. This will allow the early exit decision to occur at earlier layers in cases where the reference token sequence is accurate or nearly accurate.

The goal in this reference token-based early exit decision is not to necessarily find the best token to output, but to validate whether the current reference token is "good enough" to be a valid output token in the current sentence. Rather than change the token to an optimal one according to the model, this method can detect cases where the current reference token is adequate and, in such cases, may stop quickly and efficiently. Note that in some cases, the token considered optimal by the transformer architecture may actually be non-optimal in terms of other criteria anyway. In any case, the efficiency improvement may override accuracy criteria.

This novel early exit criteria will be efficient when the reference token is accurate. In such cases, the model's predicted token and the reference token will match, and the model can exit very early. For example, if the model's predicted token is above 20% probability and it matches the reference token's value, then the model can exit earlier than normal, even though it is not 90% certain. Overall, any reference token sequence with accurately predicted tokens will have a high rate of early exiting. Hence, the method will be very fast on accurate or near-accurate reference tokens, such as in speculative decoding if the draft model has near-correct predicted draft tokens.

In cases where the current reference token is not acceptable, then the decision logic will report a low probability and too-high top-N value for that token, and the model layers will be executed to find the best output token. The reference token and predicted output token will not match at any layer, and the model may finish processing the remaining layers, which is inefficient. However, since inaccurate reference token predictions are assumed to be relatively infrequent compared to correct reference token predictions, early exits of layers should be common with full layer executions uncommon. Hence, the algorithm is much more efficient on average with many layer computations skipped.

Furthermore, in such cases of an inaccurate reference token prediction, the general early exit criteria can still trigger, such as when the model has a high-enough confidence that its predicted output token is accurate. A variation of early exit to address this inefficiency is to combine the basic early exit decision logic with this input-specific early exit decision logic. For example, where the model is reporting consistently that the current reference token is not "good enough" to allow early exit, with another token being recommended as the highest probability, the method could still exit the layers with a different output token, without calculating all layers of the model. For example, if the model's predicted output token doesn't match the reference token, but the predicted probability of an alternative output token is above a 90% threshold, then the model can exit early and emit the predicted output token. Similarly, if the probability or top-N ranking of the reference token is too low after a reasonable number of layers, the method could make the decision that it is likely an incorrect reference token, and then choose one of the better tokens as recommended by the model in the logits.

The novel methods presented herein include: (a) adding early exiting to parallel decoding, (b) early-exit decision logic based on reference tokens, and (c) combined parallel decoding with reference-token based early exit decision logic, all have hyper-parameters such as thresholds or top-N ranking values. For example, the threshold for an output token could be 0.5% probability or higher than top-200 ranking. Although these methods can be performed with many reasonable settings, the optimal value of these hyper-parameters may vary according to the precise use cases, the chosen transformer architecture and LLM, and the input prompt characteristics.

Furthermore, there are multiple criteria to be assessed in determining what is optimal, such as there is a trade-off between processing speed and output accuracy. The characteristics of the algorithm in terms of speed versus accuracy may vary with different projects. Testing with well-known benchmarking data sets, either commercial or open-source data sets, may be useful to evaluate the speed and accuracy of a transformer architecture using these new algorithms, testing different values of these hyper-parameters, so as to choose the hyper-parameter values for the project's characteristics.

All of these exit decision methods have varying speed improvements versus accuracy loss trade-offs. The presently disclosed methods speed up inference via an improved decision logic in early exit methods based on reference tokens. This offers both increased efficiency and improved output accuracy by focusing on the reference token sequence.

The novel optimizations of the parallel decoding algorithms improve on prior art decoding algorithms by: (a) executing faster in terms of total execution time; (b) processing fewer tokens overall than parallel decoding methods, thereby reducing overall compute cost; and (c) improving accuracy of results by focusing on tokens that are more likely to be accurate.

The presently disclosed improved parallel decoding algorithms have certain limitations: (a) the autoregressive decoding bottleneck is not fully alleviated, which limits the extent of parallel processing; (b) some embodiments of the method does not use lookahead to multiple future tokens, which limits accuracy in terms of multi-token outputs; (c) the decoding algorithms may not always make the best output token suggestions and can nevertheless sometimes emit inaccurate output tokens.

Detailed Description of the Drawings

The diagrams in FIG. 1 through FIG. 13 demonstrate embodiments of the present disclosure. These are now described in detail.

FIG. 1 is a high-level block diagram of a system environment for an online cloud system, in accordance with a number of embodiments of the present disclosure. Users interact with the user devices 120A and 120B, which will include methods of input and output available to users of the cloud-based AI system. Users submit inputs such as text to the input devices on user devices 120A/120B, and it is transmitted over the network 100 to the backend cloud system 110. After processing the query, either partially or fully, the backend system sends the results back to the user over the network 100 and the user receives the results of their AI requests on output displays on their user device 120A/120B.

The cloud system 110 performs the "backend" processing of the algorithm, such as by executing a transformer engine with an LLM. This cloud system comprises one or more computer servers, whether physical or virtual, each of which may contain a number of CPU components, GPU components, memory components, storage components, and other standard computer components. Cloud system servers may not have a user interface for input or output, other than via the network, although they may also have local interfaces for administrative use.

FIG. 2 is a high-level block diagram of a computer device, such as a computer server, smartphone or laptop computer, in accordance with a number of embodiments of the present disclosure. The computer device 200 comprises may be physical or virtual, and may contain a number of CPU components 230, memory components 240 (e.g., RAM memory), storage components 250 (e.g., disk drives or solid state drives), and other standard or optional computer components, such as GPU components. When used in an AI system, the transformer engine is executed, using its LLM, on the same device as one or more user input devices 210 (e.g., mouse, keyboard) and one or more output devices 220 (e.g., monitor), without sending user queries over an external network.

FIG. 3 is a block diagram of a system for transformer inference, in accordance with a number of embodiments of the present disclosure. Input requests from a user, such as text, are sent via the input module 310 to the transformer system 300 for processing, and the results are returned to the user via the output module 330. Inputs and outputs may be in the form of text, images, video, other data formats, or any combination thereof. At a high level, the transformer system 300 comprises one or more transformer engines 320 and LLM models 340. There are numerous variants and embodiments of a transformer engine 320, and various non-transformer AI engine architectures may also be used. Similarly, many LLMs may be used as embodiments, and smaller models and other non-LLM models may also be used in place of an LLM model 340 in this embodiment.

FIG. 4 is a block diagram of an input module for a transformer, in accordance with a number of embodiments of the present disclosure. Input text 400 is submitted to the tokenizer module 410, which uses the vocabulary data 417, consisting of a mapping of text strings to numeric token values, which is stored in the LLM 415. This tokenization method converts the input text into a sequence of numeric tokens, called a "token stream". There are many possible methods of implementing a tokenizer well-known in the prior art for both programming language tokenization and AI model tokenization.

This input token stream is converted to vector embeddings, where each token is represented by an embeddings vector, consisting of multiple numeric values stored in an array or vector. This is achieved by using the embedding matrix 416, stored in the LLM 415, by first converting each token into a "one-hot vector", which is a vector consisting of zero values except a one value in the index location equal to the token value. These one-hot vectors are combined to create a matrix, with one matrix row per input token value. This matrix of one-hot vectors is multiplied with the embeddings matrix via matrix multiplication in the MatMul module 420.

An efficiency improvement to this one-hot vector MatMul 420 is to note that it is equivalent to directly extracting the row or column corresponding to the token value from the embeddings matrix (depending on whether the matrix is stored in row-major or column-major order), thereby using one row or column per token. Hence, this row or column data can be directly extracted as the embeddings vector for a token, thereby avoiding a costly matrix multiplication computation.

The embeddings created by the MatMul module 420, or the optimized row/column extraction method, and may be optionally added to additional positional encodings 440. The positional encoding adds location-specific numeric values, according to the index position of a token in the sequence. There are several positional encoding methods well-known in the prior art, including the use of recurring sine and cosine functions. The positional embeddings data created by the positional encoding module 440 are added together in the matrix addition module 430 to create the final embeddings data 450.

FIG. 5 is a block diagram of an output module for a transformer, in accordance with a number of embodiments of the present disclosure. The output module works conceptually in reverse to the input module, by converting from embeddings 500 back to tokens, and then finally back to output text 550 for display. The embeddings 500 are the calculated internal output results of the transformer, or from an earlier non-final layer of a transformer if early exiting occurs.

Each embeddings vector is converted to numeric values in the unembedding MatMul module 510 using a matrix multiplication using the unembedding matrix 517 in the LLM 515. The unembedding matrix 517 can be the inverse matrix or transposed matrix of the embedding matrix 416 in FIG. 4. The output result of the unembedding MatMul module 510 is a proportional representation of the predicted tokens, but the values are not proper probabilities. These numbers are then normalized into a vector of "logits" representing the predicted probability of each token, using the Softmax module 520. The Softmax algorithm is well-known in the prior art, involving exponentiating each element of the vector, and then scaling each element using division by the sum of these exponentiated values.

The output of Softmax 520 is input to the decoding algorithm 525. Note that the "decoding algorithm" 520 is a sub-component of a "decoder" in a transformer, despite the similarity in terminology. The decoding algorithm takes as input the vector of probabilities for each of the tokens in the vocabulary, and outputs a single chosen token. Several decoding algorithms are available in the prior art, and a novel decoding algorithm method is disclosed herein. The simplest decoding algorithm is "greedy decoding" where the token with the highest probability is output, and the corresponding text string can be output immediately. A more complex decoding method is "beam search decoding" whereby the token is not output immediately, but is deferred until the beam search method has considered the probabilities of multiple possible multi-token output sequences, which is expensive to execute but can be more accurate in some cases.

The output token value that is chosen by the decoding algorithm, once it is finally approved for output, can be converted to text using the vocabulary data 516 of the LLM 515 in the untokenizer module 530. Untokenization can be efficiently implemented for a token value by using an array of text strings based on the tokens in the vocabulary data, and using the token value as an index to access into this array. The resulting text string is added to the output text 550.

FIG. 6 is a block diagram of an encoder-decoder transformer, in accordance with a number of embodiments of the present disclosure. This shows the two major components, an encoder stack 670/665 and a decoder stack 610/615, in addition to the input module 601 and output module 660.

The encoder stack consists of N "layers", the first encoder layer 670 and a number of additional layers 665. In many embodiments, each encoder layer is identical, but in some embodiments the layers may have different structure.

Encoder output 675 is the intermediate results computed by the encoder layers, as tensors or matrices in the internal embeddings format, representing the K keys data and V values data. This output of K and V data is passed from the encoder layers to the decoder layers, for use in the cross attention module 630. In many embodiments, the K and V data from the encoder may be cached using the well-known "KV cache" optimization to avoid recomputation where the data is already available.

The decoder stack also consists of N layers, the first decoder layer 610 and a number of additional decoder layers 615. The decoder layers have a different structure to the encoder layers, such as having a cross attention block 630 that receives the output from the encoder into the decoder layer. In a different embodiment using a decoder-only architecture, there is no encoder stack, and the cross attention module 630 may be removed from decoder layers.

The decoder stack may have the same number of layers as the encoder stack, or it may have a different layer depth, such as the "deep encoder, shallow decoder" architecture where the encoder stack has more layers than the decoder stack. In many embodiments, each decoder layer is identical, but in some embodiments the layers may have different structure.

There are several "add & norm" blocks in the encoder layer (603, 605) and the decoder layer (625, 635, 645). These perform two actions: (a) addition of the input and output of the block via a residual connection, and (b) normalization of the data.

The addition computation is an element-wise matrix or tensor addition of the input and output of the block. The input data is available via a Residual Connection (RC) pathway prior to the computation block.

A pathway of a Residual Connections is used at several places in the architecture, around various computation blocks in the encoder stack (681, 682) and in the decoder stack (684, 686, 687). A residual connection takes a copy of the input data prior to a computation block, and then adds it to the output of the block after the computation. This addition of the input and output via a residual connection is helpful in optimizing training by reducing or avoiding the "vanishing gradient" problem, but some embodiments dispense with residual connections. If residual connections are used in training, they are retained in the architecture for inference.

Normalization of the data may use several well-known methods from the prior art as embodiments, such as the batch normalization method ("BatchNorm") or layer normalization method ("LayerNorm"). In different embodiments of the architecture known as a "pre-norm" architecture, the normalization computation may occur prior to computation blocks on their inputs, rather than afterwards on their outputs.

The Feed-Forward Network (FFN) is a sublayer component in many transformer architectures. An encoder-decoder transformer may include the encoder FFN 604 in the encoder layers 670/665, and the decoder FFN 640 in decoder layers 610/615. The details of the FFN architecture are shown in FIG. 8 and its description. The encoder FFN 604 and the decoder FFN 640 use the same method, but with different weights.

Each encoder layer has a self attention block 602, and decoder layers also have a self attention block 620. This cross attention module is used to pay attention to token computations using data from prior layers, also using data from the KV cache, if available.

Decoder layers in the encoder-decoder architecture in FIG. 6 also have a cross attention block 630. The cross attention block in decoder layers takes inputs that are the outputs from encoder layers. Since the encoder layer attention computations are not masked, whereas the self attention modules in decoder layers are masked, this cross attention method allows the decoder to indirectly pay attention to lookahead tokens. A decoder-only transformer architecture embodiment would remove the cross attention block 630, along with the encoder layers 670/665, but would then allow lookahead attention in the prefill phase.

The details of the QKV computation for attention modules, both self attention and cross attention, is shown in FIG. 7 and its description, and the Multi-Head Attention (MHA) optimization is shown in FIG. 9 and its description. The details of the KV cache optimization for self attention and cross attention modules are also discussed in those sections.

The first steps of this method shown in FIG. 6 occur in the input module 601, which converts input text formats into numeric tokens and then into an embedding vector internal format, which is used for computations in encoder layers and decoder layers. The input module 601 is as shown in detail in FIG. 4 and the corresponding description.

The final results of the decoder layer stack at the end of a full decoder cycle are sent to the output module 660 for processing. The embeddings internal data format is converted to token formats via an "unembedding" method shown in FIG. 5 and its discussion. When executing in autoregressive decoding phase, the output token may be: (a) emitted to output text 640 by untokenization from tokens to text strings, and (b) sent along the autoregressive token pathway 650, where the new output token is added to the intermediate output 600 for use in the next full decoding cycle. The output module 660 is as shown in detail in FIG. 5 and the related description.

Another embodiment of a transformer similar to FIG. 6 is a decoder-only transformer architecture. A decoder-only transformer does not have any encoder layers 670/665, and also does not use cross attention modules 630, which are based on encoder output 675, nor does it have corresponding add/norm module 635 or residual connection 686.

FIG. 7 is a block diagram of a system for QKV attention in a transformer, in accordance with a number of embodiments of the present disclosure. This method is used to compute "attention" results in multiple parts of a transformer architecture. For example, the QKV attention method is used for the self attention modules 602/620 and cross attention module 630 in FIG. 6.

The inputs Q 700, K 701, and V 702 are data in the format of matrix or tensors, that are used to compute the "attention" weightings to give to neighboring tokens in a sequence. This method allows the transformer to understand relationships between words in a sentence or broader document text.

In a cross attention module of an encoder-decoder transform architecture using this QKV method, the K and V values come from the encoder layers output. In a self attention module of an encoder layer, the K and V data comes from a prior encoder layer. In a self attention module of a decoder layer, whether in an encoder-decoder or decoder-only transformer architecture, the K and V data comes from a prior encoder layer. In many embodiments, the K and V data will come from a "KV cache" stored in memory, if already computed by a prior computation, using the well-known KV caching optimization. In a self attention block of the autoregressive decoding phase of the decoder stack, the KV cache should contain already-computed K and V data for every token in the output token sequence, except the current output token for which its predicted probability is being calculated.

MatMul 710 performs a matrix multiplication between Q 700 and K 701, without using V 702. The output results are passed into the Scale module 720 that reduces the size of the values. In many embodiments, the scale factor is division by the square root of the internal model dimension size, which is the length of the embedding vectors.

The computed output from the Scale module 720 is passed into the Masking module 730, which is an optional module that can be skipped in some methods. When activated, the masking prevents the attention computation from "lookahead" and limits computations for a token to tokens earlier in the token sequence.

In an encoder-decoder transformer architecture, masking is disabled in attention blocks used in an encoder layer, but enabled when used within attention blocks in a decoder layer. In a decoder-only transformer architecture, masking of lookahead tokens may be disabled in the "prefill" phase at the start, and then enabled when in the subsequent autoregressive decoding phase.

The output from the Scale module 720, or its input when disabled, is passed to the Softmax module 740. The Softmax module 740 functions as already described above in FIG. 5 and its description.

The final phase of the QKV computation is the MatMul block 750, which multiplies the intermediate computations, based on Q 700 and K 701, with matrix multiplication using the data from V 702. Hence, the final result of the QKV attention block uses data from its three inputs Q 700, and K 701, and V 702.

FIG. 8 is a block diagram of a Feed-Forward Network (FFN) module, also known as a Multi-Layer Perceptron (MLP), in accordance with a number of embodiments of the present disclosure. The FFN components are heavy computation phases in the transformer engine execution. The basic architecture of the FFN involves sending the FFN input tensor data 800 to a first linear layer 810 (using the first set of FFN weights and biases 820), an activation function module 830, and then a second linear layer 840 (using the second set of FFN weights and biases 821). Finally, there is an addition module 850 using the data from the FFN input tensor 800 via residual connection 855.

Each linear layer comprises a matrix multiplication operation using the corresponding weight matrix, optionally followed by addition of a bias vector, where each linear layer has its own specific set of weights and biases stored in the LLM.

Residual connection 855 sends a copy of the input tensor data 800 to be used after the two linear layers in the addition module 850. The use of an added input via a residual connection has been shown to be advantageous in training models, and is also calculated during inference.

The addition module 850 adds the output of the second linear layer 840 to the original inputs to the FFN module, thus adding the inputs and preliminary outputs to create the final output of the FFN module. This arithmetic addition method uses element-wise tensor or matrix addition of each pair of values.

The FFN is one of the major sublayer components in the layers of encoders and decoders. The encoder FFN 604 and the decoder FFN 640 in FIG. 6 use this FFN architecture.

FIG. 9 is a block diagram of a Multi-Head Attention (MHA) module, in accordance with a number of embodiments of the present disclosure. This MHA method is a well-known optimization to the QKV attention computations in FIG. 7 The use of a MHA architecture facilitates parallelization of the computations in an attention block, such as a self attention block or cross attention block. The computation is split across H different blocks called "attention heads." Parallelized computation allows faster execution on GPU hardware or software threads.

The Scaled Attention block 920 and the linear layers (910, 911, 912) perform attention computations via matrix/tensor multiplications in accordance with Q 902, K 901 and V 900 tensors, as shown in FIG. 7 and its description.

The concatenate block 930 merges the outputs of the H attention heads into a single tensor result. Another linear layer 940 is applied to finalize the QKV computations for attention using a matrix and bias data, similar to the MatMul block 750 in FIG. 7.

The output of this MHA block is to be a faster way to compute a result that is identical or near-identical to the output of a single attention computation, as shown in FIG. 7, if it were computed on the whole data without parallelization.

FIG. 10 is a flow-chart of a method for autoregressive decoding in a transformer, in accordance with a number of embodiments of the present disclosure. A full decoding cycle is the execution of the layers of the decoder stack 1010 (or fewer layers if an early exit triggered) so as to output a single token. An autoregressive transformer performs one cycle per output token, in sequential execution (i.e. not parallel execution), outputting one token at a time. At the end of each decoding cycle, the output module 1020 chooses a new output token, and this newly output token and its embeddings data is sent down the autoregressive pathway 1030, where it is added to the intermediate output 1000, to be used as input to the first decoder layer in the next full decoder cycle.

The details of the decoder layer stack 1010 are shown in FIG. 6. Similarly, not all details of the output module 1020 are shown, as they have already been examined in FIG. 5. The output module will also include an unembedding module, Softmax module, untokenizer module and a decoding algorithm module to choose the token, including the many well-known decoding algorithms.

In addition to forwarding the new token to be used autoregressively, the output module 1020 may convert the token to text, and add it to the output text 1040. With simple decoding algorithms such as greedy decoding, the text is output immediately. In more advanced decoding algorithms, such as beam search decoding, the text output is deferred until the decoding algorithm makes additional computations as to which token or token sequence to finally output.

FIG. 11 is a flow-chart of a method for early exit optimization of a transformer, in accordance with a number of embodiments of the present disclosure. The early exit module will stop executing further layers of the decoder stack, if conditions are met, thereby avoiding much computation and improving efficiency. The early exit test 1140 makes the decision whether or not to exit processing at the current decoder layer. If the pathway is Yes 1141, then further decoder layers are not executed, and the decoding module 1150 performs the end-stage of a full decoding cycle. If the pathway chosen is No 1142, then processing continues as usual to the next layer in the decoder stack.

The input to the early exit module is the output of a decoder layer in an embeddings data format. This embeddings data is converted to token probabilities ("logits") using the unembedding module 1110, which converts to non-normalized internal numeric values, and then the Softmax module 1130, which converts to token probabilities. The output of Softmax is logits that are normalized with each value within the range [0,1], inclusive, and logit values properly sum to one. The details of the unembedding module 1110 and Softmax module 1130 have already been described in FIG. 5 and associated discussion.

There are several embodiments of methods for the early exit test 1140 in the prior art, including several methods based on: (a) no token probabilities, or (b) computation of the probabilities of the tokens. For example, no token probabilities are used to exit after executing a fixed number of layers, or after a fixed percentage of layers, such as exiting after 50% of layers. As an alternative example, the token probabilities (or at least, their unembedding values) may be computed so as to find the token with the highest probability.

Note that early exit criteria based on the maximum of the token probabilities, or also the second highest or top-k highest values, could be optimized to avoid the Softmax computation, by using the maximum tests on the pre-Softmax values after the unembedding computation. The maximum pre-Softmax value token will also have the maximum Softmax-computed probability, as will the second-highest, and so on, because the exponentiation function used in Softmax is a monotonically increasing mathematical function.

Some simple types of early exit decision criteria do not use the probabilities of all tokens. For example, early exiting after a fixed number of layers is a simple comparison between the layer count and a fixed constant, without considering any token probabilities. Another variant would be two fixed layer counts, with different values for the encoder stack versus the decoder stack in an encoder-decoder transformer architecture, or differing for the prefill phase versus the decoding phase in a decoder-only transformer. Note that the early exit test is also trivial at the final layer of the decoder stack, as further processing of decoder layers cannot occur in any case.

If the early exit decision criteria is a simplistic method, such as executing after a fixed number of layers, then the unembedding module 1110 and Softmax module 1130 are not used to evaluate the early exit test 1140, but will be subsequently used in the decoding module 1150 if an early exit of layers is triggered.

The decoding module 1150 is executed if early exit of layers is triggered by the Yes pathway 1141. This decoding module includes various modules already described in earlier figures, including a decoding algorithm, untokenization, and an autoregressive token pathway. If the unembedding module 1110 and Softmax module 1130 have already been computed prior to evaluating the early exit test 1140, then the decoding module 1150 may not re-compute the unembedding or Softmax computations because these have already been performed in the early exit pathway.

If the early exit test 1140 fails, then the No pathway 1142 is executed, which continues execution of the next decoder layer 1145. If the early exit test 1130 has decision criteria that only consider the current layer of logits, then the outputs of the unembedding module 1110 and Softmax module 1130, if any, are discarded, which is an inefficiency. However, these values may be retained in memory for use in a future test by the early exit test module 1140, if the early exit decision criteria involve probabilities from prior layers. If the early exit criteria are simplistic tests not involving logits, such as a fixed number of layers, then there are no values computed by the unembedding module 1110 and Softmax module 1130, and nothing needs to be stored.

FIG. 12 is a flow-chart of a method for speculative decoding of a transformer, in accordance with a number of embodiments of the present disclosure. The method of speculative decoding is shown as one embodiment, and other embodiments via modifications to this flow-chart are also described below to demonstrate lookup decoding, aggressive decoding, blockwise parallel decoding, and other types of parallel decoding.

The two main parts of speculative decoding are the draft transformer 1250, which generates the draft tokens as a reference token sequence, and the verifier transformer 1260, which verifies the correctness of the reference tokens. As already discussed, the draft transformer is usually a smaller and faster transformer than the verifier transformer. The details of a speculative decoding method are now described.

The input text from a prompt is processed by the input module 1210. The details of the input module have been described in FIG. 4 and associated discussion. At the start of processing, the more tokens test 1220 is trivially true and execution continues along the Yes path 1222 into the reference token generator 1240.

The reference token generator 1240 uses the draft transformer 1250 to generate a number of draft tokens, or reference tokens, in a sequence, creating a reference token sequence. In many embodiments, the reference token generator 1240 uses a sequential method of repeatedly calling the draft transformer 1250, using an autoregressive algorithm, whereby each generated draft token is appended to an intermediate token sequence, and then sent to the next call to the draft transformer 1250 as part of its input, repeating this autoregressive process until no further tokens are required. However, in some embodiments the draft transformer 1250 may use a parallel method of generating multiple draft tokens, and the reference token generator 1240 would make fewer calls, or only one call, to the draft transformer 1250.

In many embodiments, the draft transformer 1250 uses a small, efficient neural network model, such as a reduced-size LLM, called a "small language model," that is processed by a transformer engine using an autoregressive method (i.e., it's a smaller and faster version of the bigger verifier transformer 1260). However, in other embodiments, various other methods, including different types of models with different transformer architectures, or other non-transformer architectures, are used to generate draft tokens, by predicting what the next token of the draft token sequence is likely to be.

The verifier transformer 1260 receives each of the reference tokens, and generates a subsequence ending with each reference token, one subsequence per reference token, to analyze separately. Each of these subsequences is processed with a full cycle of transformer inference using the verifier transformer 1260. In many embodiments, the verifier transformer 1260 will perform these full inference cycles in parallel for all of the reference tokens (as indicated by multiple arrows on the flow-chart), but other embodiments could use sequential processing or a combination of parallel and sequential processing.

The evaluator module 1270 receives the results of inference by the verifier transformer 1260 for the sequences ending with each reference token. In many embodiments, these results would be received from parallel computation (as indicated by multiple arrows on the flow-chart), but other embodiments could use sequential processing. It determines the maximum prefix subsequence of the reference tokens (e.g., draft tokens) that are accepted, and sends one or more tokens to the output module 1280, but discards the remainder of the unaccepted reference tokens. For the first reference token that is rejected by the evaluator, it can be replaced by another token according to a standard decoding algorithm, such as greedy decoding or top-k decoding, using the logits for that reference token position. This can also be done for the very first reference token if all tokens are rejected, thereby always outputing at least one token, and avoiding the infinite loop that would result if zero tokens were output.

The output tokens module 1280 outputs one or more tokens from the evaluator module 1270 to the output text using untokenization methods, and also sends them on the autoregressive pathway to the more tokens test 1220. The output module has been shown in earlier figures, such as FIG. 5 and related discussion. The main difference in speculative decoding is that it may output multiple tokens, and hence its actions may be repeated on multiple tokens. The output module 1280 may not need to calculate unembedding and Softmax calculations if these have already been performed in the evaluator module 1270.

When output tokens are sent along the autoregressive pathway, the more tokens test 1220 determines if processing should stop, such as by tracking token counts, maximum token configurations, or watching for a stop token in the output tokens. If there are more tokens or processing should continue, the Yes path 1222 is followed and the above steps are repeated for another cycle of speculative decoding. If there are no further tokens to process or otherwise termination is indicated, execution follows the No path 1221 and the method finishes in the end module 1230.

In lookup decoding as another embodiment, the draft transformer 1250 is replaced by a retrieval mechanism, whereby recently output tokens are used to search documents or excerpts of documents, for subsequences within the document tokens for a matching token subsequence, and the reference tokens are available all at once from this subsequence. Such documents or texts are tokenized, so as to search by tokens effectively. There are many possible embodiments of a retrieval system, such as a datastore or database. The rest of the lookup decoding method (with retrieval) works as for speculative decoding, including its many embodiments.

In prompt lookup decoding as another embodiment, the draft transformer 1250 is replaced by a token search method, whereby the recently output tokens are searched for in the input tokens. A subsequence of the input tokens is then returned as the reference tokens, and multiple reference tokens are available immediately from this subsequence. The rest of the prompt lookup decoding method (with search) works as for speculative decoding, including its many embodiments.

In blockwise parallel decoding as another embodiment, the draft transformer 1250 is replaced by a non-autoregressive transformer architecture using a small model. This non-autoregressive method outputs multiple draft tokens in parallel, which are received by the reference token generator 1240, as already described. The rest of the blockwise parallel decoding method works as for speculative decoding, including its many embodiments.

In aggressive decoding as another embodiment, the draft transformer 1250 is replaced by a module that uses a sub-sequence of the input token sequence as the reference tokens. Hence, there is not a transformer or a model in this modified module. This modified module may incrementally track the location in the input sequence to use as the start of the subsequence, or it may use a search method to find the current subsequence of input tokens to be used as reference tokens. The rest of the aggressive decoding method works as for speculative decoding, including its many embodiments.

The diagram in FIG. 13, and also the combination of diagrams from FIG. 12 and FIG. 13, show novel aspects of the methods and apparatuses in embodiments of the presently disclosed invention, including a combined parallel decoding and early exit method, and a further optimized method of early exit based on the current reference token.

FIG. 13 is a flow-chart of a novel improvement for the early exit method, extended by current reference token decision optimization, in accordance with a number of embodiments of the present disclosure. Prior art methods of early exit do not take advantage of the extra information available from reference tokens, such as the draft tokens in speculative decoding. Basing the early exit decision on both the computed logits and the probability of the reference tokens allows for: (a) greater efficiency by early exiting the decoder stack more often and at lower layers, thereby skipping more layers of computation in total, and (b) improved accuracy by focusing on reference tokens that are already considered likely to be output by the method that generated the reference tokens (e.g., a smaller model in speculative decoding).

Much of FIG. 13 is similar to FIG. 11, which shows the early exit method, but with an extra current reference token testing module 1340. This improved early exit module has two exit tests: (a) the new current reference token test 1340, and (b) the general early exit test module 1343, with decision logic based on the probabilities of the tokens. If either of these tests succeed, the layers exit early and results are sent to the decoding module 1350.

The current reference token test 1340 determines the current reference token from the reference token sequence 1320. If the early exit reference token test 1340, using the current reference token succeeds, execution follows the Yes path 1341 with early exiting triggered and the decoding module 1350 will finalize the output of the decoding cycle. In basic early exit, the decoding module 1350 will convert the output token to output text 1360, as well as sending the token down an autoregressive pathway for the next full decoding cycle. In speculative decoding using this reference token early exit test 1340, this decoding module 1350 will perform the evaluation of the results from processing all the reference tokens, whether in parallel or sequentially (i.e., the decoding module 1350 will act as one of the inputs to the evaluator module 1270 in FIG. 12).

The current reference token test 1340 is placed before the early exit all tokens text 1343. If the current reference token test 1340 fails, execution follows the No path 1342 and a follow-up general all tokens early exit test 1343 is performed, which uses computed logits without the reference token sequence.

The comparison used in the current reference token test 1340 can be a simple arithmetic operator, a more complicated mathematical expression, or a sequence of arithmetic tests and conditions. Various methods of using the current reference token and its probability in the current reference token test 1340 include: (a) a threshold probability is exceeded by the current reference token (e.g., the current reference token has a probability at 20% or more); (b) current reference token ranking is below a ranking threshold based on the inverse of a threshold probability (e.g., the current reference token's ranking is less than 5, which is the inverse of 20%); (c) current reference token has the maximum predicted probability; (d) current reference token is one of the top-k predicted output tokens in terms of relative probabilities (e.g., k=2 means the token has maximal or second-highest probability); or (e) a combination thereof. An example of a combination would be to use the current reference token if it has maximum predicted probability, and also exceeds a lower-bound 20% probability threshold.

The decoding module 1350 includes various modules already described in earlier figures, including a decoding algorithm, untokenization, and an autoregressive token pathway. However, it does not calculate its own unembedding or Softmax outputs if these have already been calculated in the early exit pathway.

The all-tokens early exit module 1343 has already been described, including versions requiring all logit probabilities and simpler versions not requiring any probabilities. The all-tokens early exit module 1343 may have any or all of the features described for the early exit decision module 1140 in FIG. 11.

Another embodiment of this method is to use different acceptance calculations at the current reference token test 1340 for different decoder layers. The predictions of many models become more accurate after each layer. Early layers tend to roughly compute the general probabilities, middle layers are sorting out the hierarchy and longer context relevance, and the final layers tend to finesse between various acceptable candidates. Furthermore, so-called "easy" tokens tend to be chosen early, whereas "hard" tokens don't get chosen until later layers. Hence, it would be appropriate to make the criteria more difficult to pass in the early layers, but easier in the higher layers.

This use of layer-specific criteria at the current reference token test 1340 is both efficient and accurate, by allowing early exit quickly in a lower layer if the prediction is "easy" and has a high probability in early layers, whereas "difficult" tokens would be rejected until later layers, but could still exit earlier in the middle or final layers. For example, three threshold percentages could be used to test the current reference token probability, representing thresholds for the early, middle, and later layers of the decoder stack. In the general case, completely different criteria with different thresholds could be used for every layer.

Another further embodiment of this method is to extend the current reference token test 1340 to use early exit acceptance criteria based on multiple reference tokens from the reference token sequence. For example, the acceptance criteria for the current reference token could also consider in its calculations the probability or ranking of the previous reference token, or the next reference token. As another example, the criteria could include whether or not the prior reference token was accepted and output..

It is efficient to put the current reference token test 1340 before the all-tokens early exit test 1343 because: (a) it is a "common case first" optimization because it is more likely to succeed at an earlier layer; and (b) it is a "simple case first" optimization if the current reference token test 1340 does not use any linear-complexity operations, such as maximum or top-k calculations, such as where the test is based on comparing the probability of the current reference token against a fixed threshold value, which can be computed in constant time complexity.

An optimized version of the current reference token exit test 1340 is available where it exits early if the current reference token is also the highest-probability predicted token, or in the highest top-k tokens. For these tests, it is possible to avoid executing the Softmax module 1330 and analyze the output values of the unembedding module 1310. The calculated numeric values from the unembedding module 1310 are log-scale values for each token, which are of unclear significance versus exact probabilities, but are nevertheless indicative of relative magnitudes because exponentiation is a monotonically increasing mathematical function. Hence, in this circumstance, the current reference token exit test 1340 could compute either the maximum of the unembedding values, or the top-k of such values, in order to decide on the current reference token early exit test 1340 without needing Softmax calculations. Although efficient for a maximum or top-k early exit decision test against the current reference token, this optimization does not allow a threshold test against the actual probability of the current reference token.

A minor optimization to this novel early exit method is computing the current reference token value at the start of each decoding cycle, if possible, or at the very first early exit decision, if possible. This avoids the re-calculation of this value at every current reference token test 1340 at different layers within the same decoding cycle. However, the probability or ranking of the current reference token is re-calculated at every layer where there is an early exit test.

The novel early exit method may be combined with certain types of parallel decoding algorithms, where a reference token sequence is available in such methods, by adding the novel optimization to the method shown in FIG. 12. The extra information available as a reference token sequence offers the ability to use reference tokens in the optimized early exit algorithm, thereby speeding up the verifier transformer 1260 Such methods that offer a reference token sequence include: (a) speculative decoding (using the draft token sequence generated by a small model as the reference token sequence), (b) lookup decoding, using a subsequence of external documents as the reference token sequence; (c) prompt lookup decoding, using a subsequence of the input prompt context tokens as the reference token sequence; (d) blockwise parallel decoding, using a non-autoregressive transformer model to generate multiple draft tokens in parallel as the reference token sequence; (e) aggressive decoding, using a subsequence of the input tokens as the reference token sequence; and (f) any other embodiments that are variants of these methods, or are other decoding algorithms whereby a reference token sequence is available.

The advantages of this novel method combining an advanced early exit method with parallel decoding algorithms involve: (a) reduced parallel computation, and (b) sequential execution is possible.

Parallel execution of these parallel decoding algorithms is improved because the main transformer inference phase may early exit, thereby avoiding layers of computation, which are often many millions of arithmetic operations. When performed in parallel across multiple reference tokens, each parallel invocation of a reference token may exit at a different layer, but the overall amount of computation will be reduced. The wall clock speed will be limited by the parallel invocation that performs the most layer computations, possibly all layers, but the overall data center cost of the GPU processing load will be reduced, even if one or more reference tokens is "difficult" and requires all layers to be computed.

Sequential execution is also improved by using the novel early exit extensions applied to these parallel decoding algorithms. Paradoxically, the so-called "parallel" decoding algorithms no longer need to be executed in parallel to be beneficial. The extra overhead of the draft model or other reference token sequence generation can be exceeded by the efficiency gain from exiting early with higher probability, thereby avoiding sequential computations of model layers. Hence, sequential execution may possibly benefit from this optimization, which means that on-device execution on low-resource platforms such as laptops and smartphones may be improved by this technique.

Furthermore, in a fully sequential execution, the reference token sequence need only be a single reference token, because there is no need to analyze more than one reference token in parallel. In fact, using a single reference token may be desirable, as this avoids any wasteful computation for reference tokens beyond the first one that is rejected (i.e., the discarded reference tokens in the parallel decoding algorithms). For example, if two reference tokens are generated, and the first reference token is rejected by the verifier transformer 1260, then the computation of the second reference token by the draft transformer 1250 is wasted.

There are several limitations of the novel methods disclosed herein as optimizations of certain parallel decoding algorithms. Not all types of decoding algorithms can be optimized in this way using an early exit improvement, because not all decoding algorithms make use of a token sequence that can be used as the reference token sequence inside the early exit decision module. All of these methods have some extra calculation performed to create the token sequence to use as a reference token sequence, so this computation overhead needs to be less than the computation gain from using improved early exit in the main transformer. Any type of early exit is an approximation, which can reduce the accuracy of the output tokens, but the modified early exit method is more accurate than an unimproved early exit method, because it can focus on the reference tokens, which are intended to be likely candidates for output.

Summary

For the purposes of interpretation of the description herein, the designatory term "a number of" means one or more, a "plurality" means two or more, and a numeric designation such as "N" of an element means a number of such elements. Where the same designator has been applied to different elements, this does not imply that they must have the same number.

The foregoing description of the embodiments of the invention has been presented for the purpose of illustration and is not intended to be exhaustive or to limit the invention to the precise forms described herein. Persons skilled in the relevant art can appreciate that many modifications and variations are possible in light of the above disclosure. Elements shown in the various embodiments herein may be added, modified, exchanged, and/or eliminated so as to provide a number of additional embodiments of the present disclosure. Adaptations, variations and/or alternative methods of implementing elements in the disclosure that produce the same results can be substituted for the specific embodiments herein.

Numerous specific features of the embodiments have been disclosed in the descriptions and drawings, in order to provide context for a thorough understanding. However, some well-known or conventional details are not described in order to provide a concise discussion of embodiments disclosed herein.

Various features are grouped together in a single embodiment in the descriptions herein for the purposes of streamlining the disclosure. This manner of disclosure is not to be interpreted as reflecting an intention that the disclosed embodiments have to use more features than are expressly recited in each claim.

Some portions of this description describe the embodiments of the invention in terms of algorithms and symbolic representations of operations on information. These algorithmic descriptions and representations are commonly used by those skilled in the data processing arts to convey the substance of their work effectively to others skilled in the art. These operations, while described functionally, computationally, or logically, are understood to be implemented by computer programs or equivalent electrical circuits, microcode, or the like. Furthermore, it has also proven convenient at times, to refer to these arrangements of operations as modules, without loss of generality. The described operations and their associated modules may be embodied in software, firmware, hardware, or any combinations thereof.

Any of the steps, operations, or processes described herein may be performed or implemented with one or more hardware or software modules, alone or in combination with other devices. In one embodiment, a software module is implemented with a computer program product comprising a computer-readable medium containing computer program code, which can be executed by a computer processor for performing any or all of the steps, operations, or processes described.

Embodiments of the invention may also relate to an apparatus for performing the operations herein. This apparatus may be specially constructed for the required purposes, and/or it may comprise a general-purpose computing device selectively activated or reconfigured by a computer program stored in the computer. Such a computer program may be stored in a non-transitory, tangible computer readable storage medium , or any type of media suitable for storing electronic instructions, which may be coupled to a computer device bus. Furthermore , any computing systems referred to in the specification may include a single processor or may be architectures employing multiple processor designs for increased computing capability.

Embodiments disclosed herein are not described with reference to any particular programming language. A variety of programming languages may be used to implement the methods and apparatuses.

Although embodiments disclosed above may described with some sequential steps, some such operations may be performed in a different order, or with some steps performed in parallel by software or hardware.

Embodiments of the invention may also relate to a product that is produced by a computing process described herein. Such a product may comprise information resulting from a computing process, where the information is stored on a non transitory, tangible computer readable storage medium and may include any embodiment of a computer program product or other data combination described herein.

Finally , the language used in the specification has been principally selected for readability and instructional purposes, and it may not have been selected to delineate or circumscribe the inventive subject matter. It is therefore intended that the scope of the invention be limited not by this detailed description, but rather by any claims that issue on an application based hereon. Each of the following claims are hereby incorporated into the detailed description as a separate embodiment. Thus, the disclosure of the embodiments of the invention is intended to be illustrative, but not limiting, of the scope of the invention, which is set forth in the following claims.

CLAIMS

What is claimed is:

1. A method for performing inference in a neural network system, comprising the steps of:
   (a) calculating a reference token sequence;
   (b) performing a layer computation of a neural network model;
   (c) calculating information about one or more predicted output tokens using the layer computation;
   (d) calculating information about one or more reference tokens using the layer computation;
   (e) performing a comparison of the reference token information to the output token information;
   (f) determining whether or not to skip further layers based on the comparison; and
   (g) determining whether or not to output the current reference token based on the comparison.
2. e The method of Claim 1, wherein the neural network system comprises an encoder-only transformer architecture.
3. The method of Claim 1, wherein the neural network system comprises a decoder-only transformer architecture.
4. The method of Claim 1, wherein:
   (a) the neural network system comprises a decoder-only transformer architecture; and
   (b) the layer computation occurs in the prefill phase.
5. The method of Claim 1, wherein:
   (a) the neural network system comprises a decoder-only transformer architecture; and
   (b) the layer computation occurs in the decoding phase.
6. The method of Claim 1, wherein the neural network system comprises an encoder-decoder transformer architecture.
7. The method of Claim 1, wherein:
   (a) the neural network system comprises an encoder-decoder transformer architecture; and
   (b) the layer computation occurs in an encoder layer.
8. The method of Claim 1, wherein:
   (a) the neural network system comprises an encoder-decoder transformer architecture; and
   (b) the layer computation occurs in a decoder layer.
9. The method of Claim 1, wherein the reference token sequence is generated by a neural network model.
10. The method of Claim 1, wherein the reference token sequence is generated by a method other than a neural network model.
11. The method of Claim 1, wherein the reference token sequence is generated from one or more document sections found by searching in a retrieval system .
12. The method of Claim 1, wherein the reference token sequence is generated by searching the input token sequence.
13. The method of Claim 1, wherein the reference token sequence is the input token sequence.
14. The method of Claim 1, wherein the comparison involves the relative ranking of the reference tokens and the output tokens.
15. The method of Claim 1, wherein the comparison involves the predicted probabilities of the reference tokens and the output tokens.
16. The method of Claim 1, wherein the comparison involves comparing the predicted probability of the reference tokens with a threshold.
17. The method of Claim 1, wherein the comparison involves comparing the relative ranking of the reference tokens with a threshold.
18. The method of Claim 1, wherein the inference is performed for grammatical error correction.
19. The method of Claim 1, wherein the inference is performed for on-device inference.
20. The method of Claim 1, wherein the inference is performed on a cloud system.

DRAWINGS

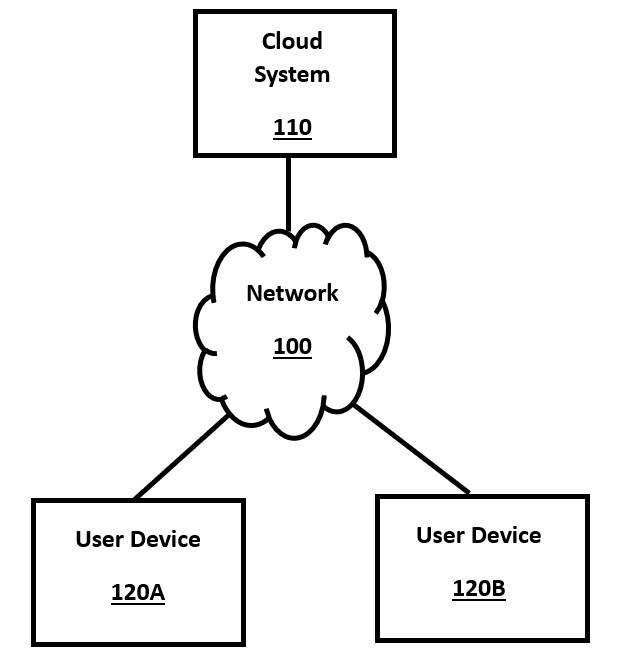
              FIG. 1

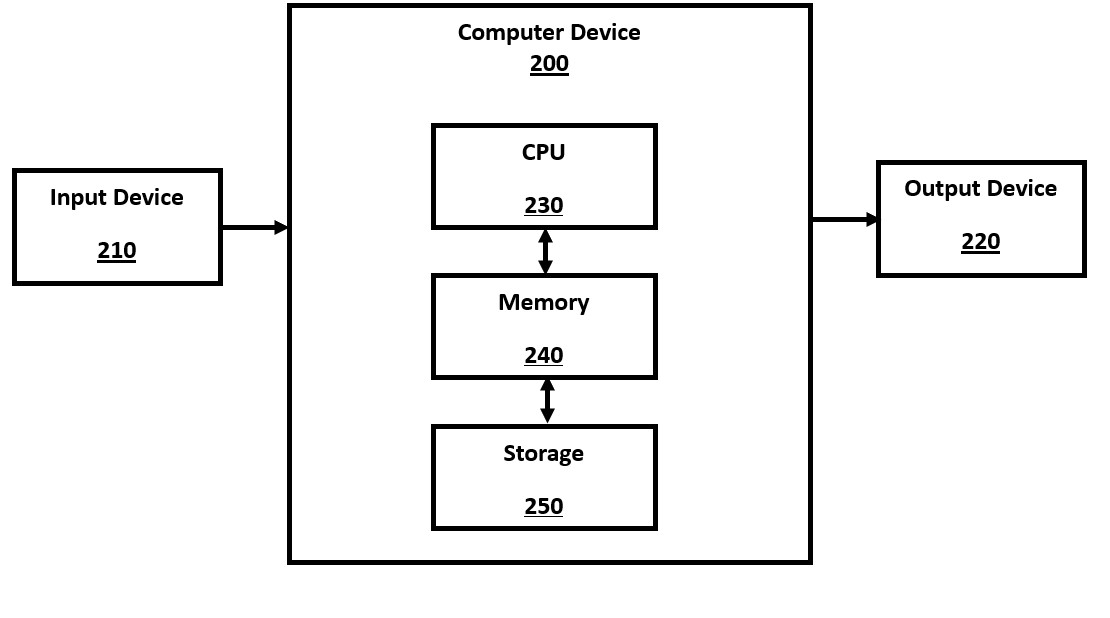
              FIG. 2

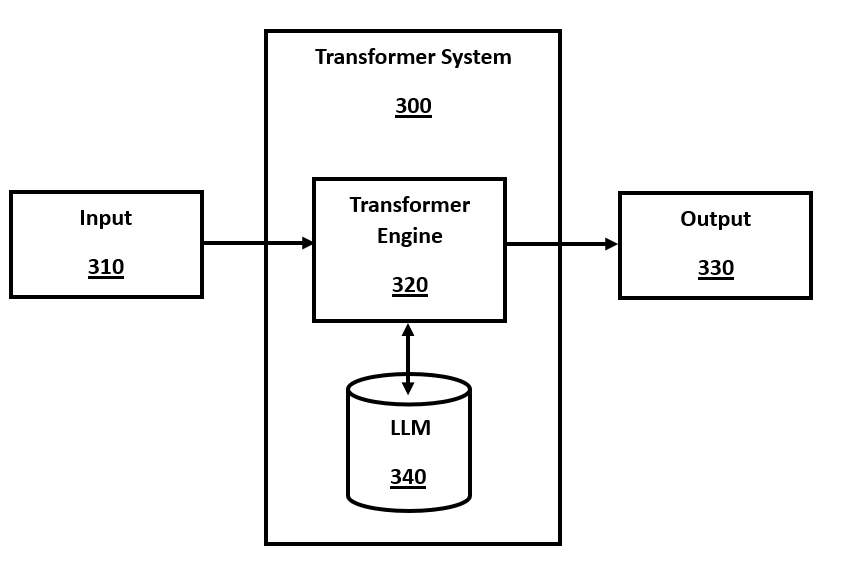
              FIG. 3

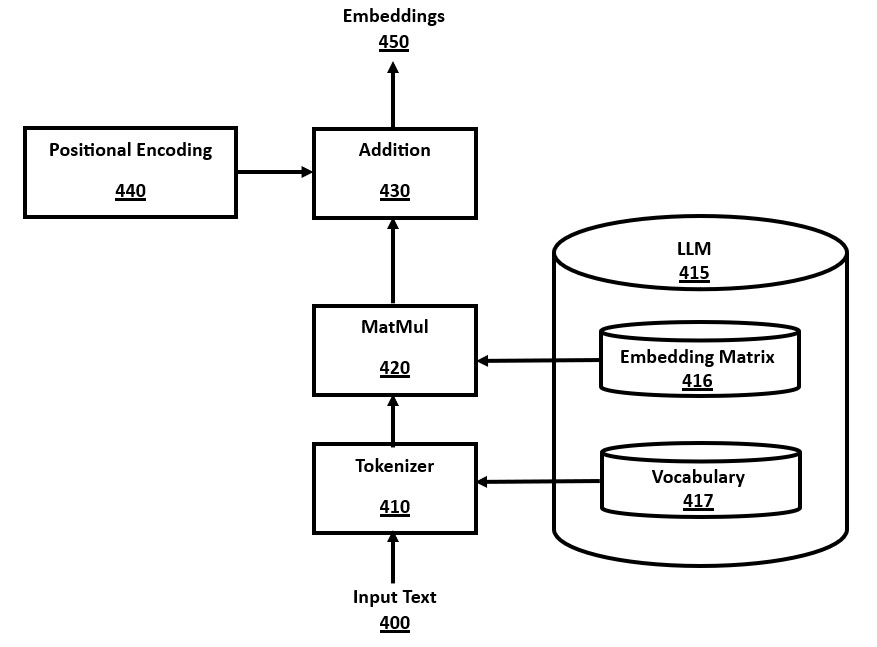
              FIG. 4

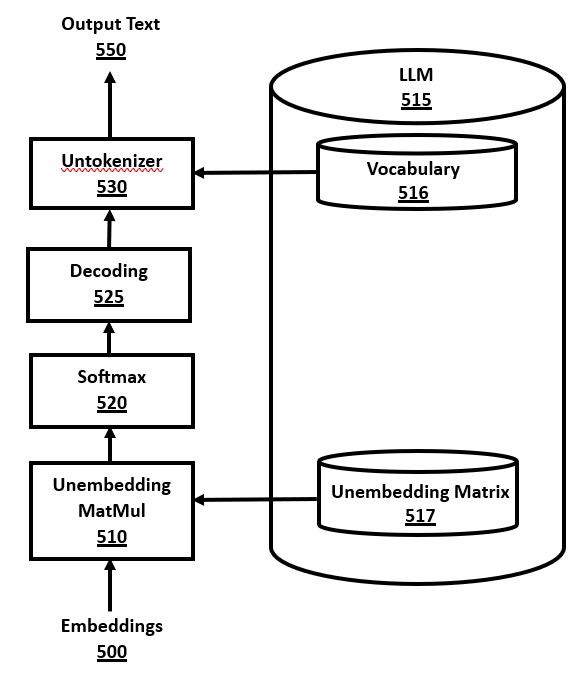
              FIG. 5

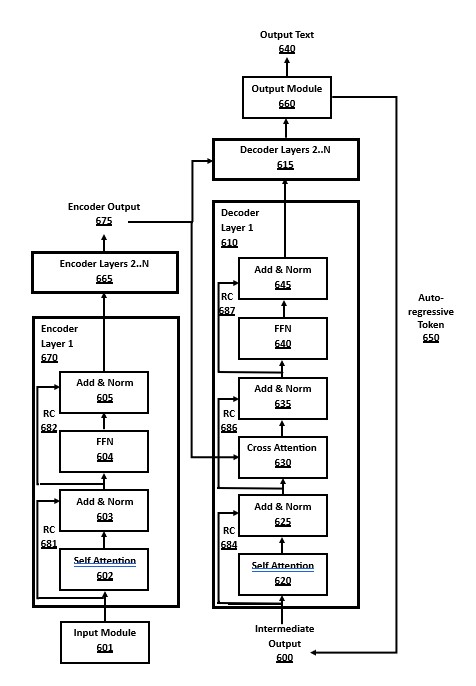
              FIG. 6

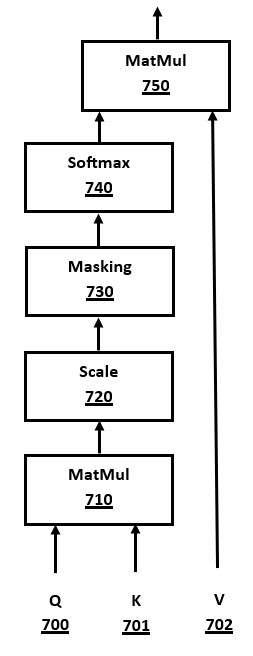
              FIG. 7

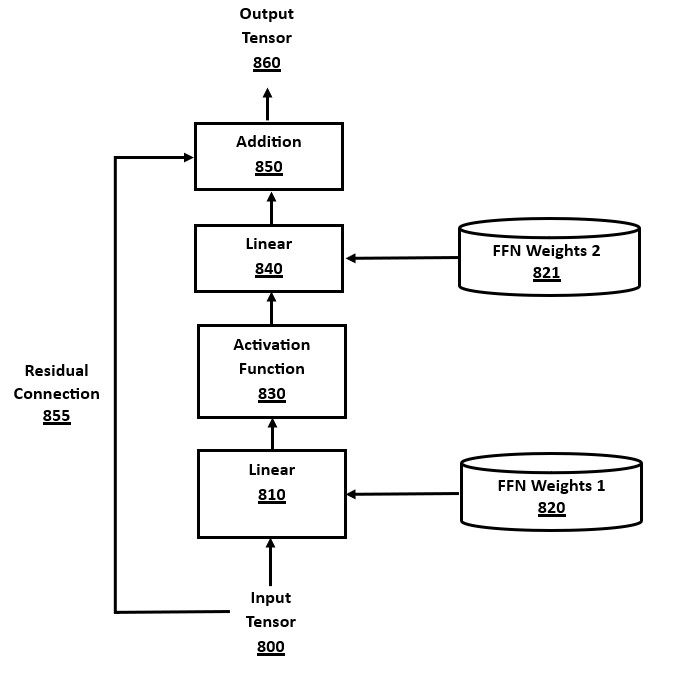
              FIG. 8

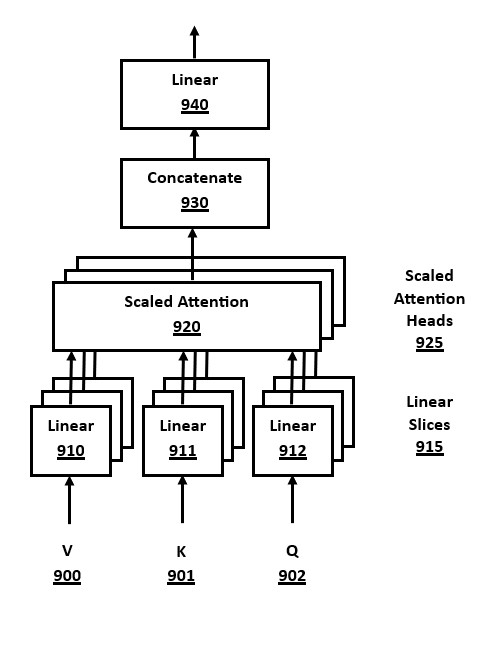
              FIG. 9

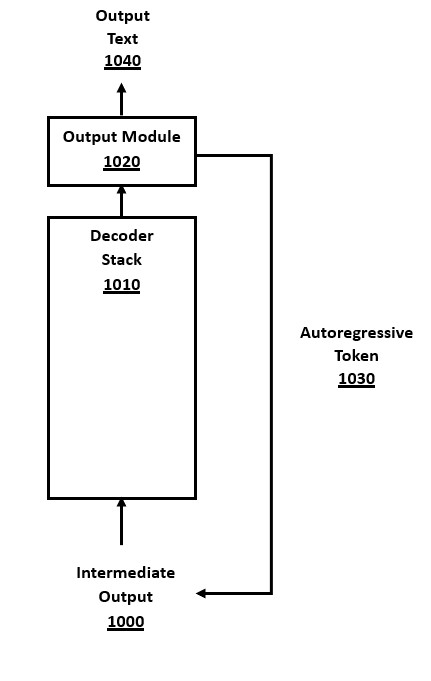
              FIG. 10

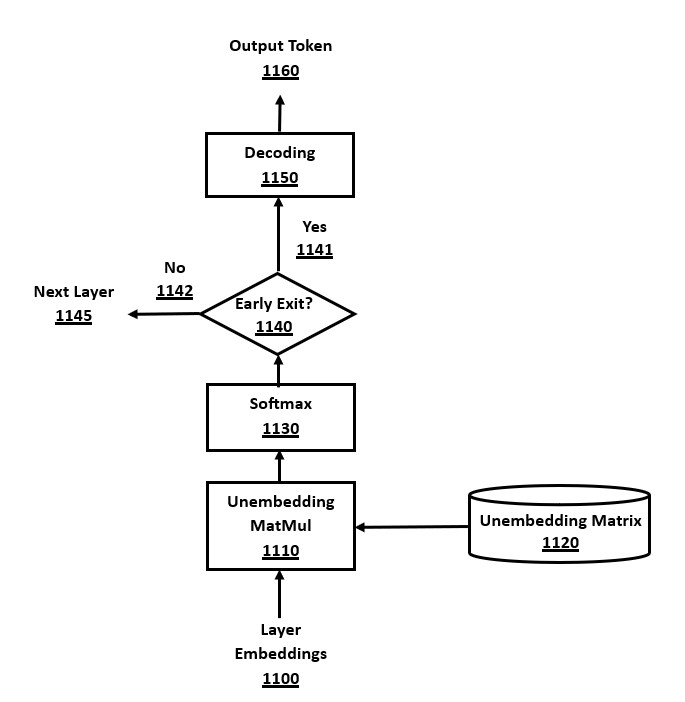
              FIG. 11

              FIG. 12

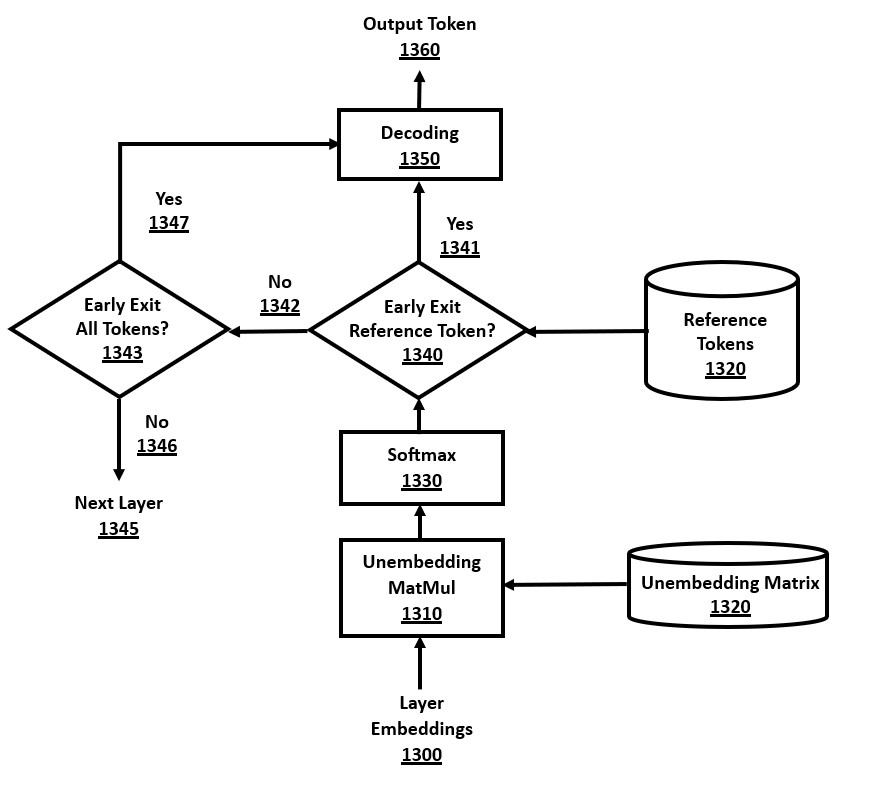
              FIG. 13